Appendre les séries mathématiques numériques (lien sur Wikipédia) dans les premières années universitaires est un passage obligé pour les étudiants techniques en général et les étudiants en informatique en particulier. Ça permet spécifiquement aux informaticiens et aux machines informatiques d’utiliser les séries comme des fonctions génératrices, pour calculer les fonctions dites non numériques, comme par exemple le cosinus, le sinus, la tangente, le logarithme, l’exponentielle…etc, qui ne sont pas décrites numériquement en utilisant le plus, le moins, la multiplication, la division…etc, donc a priori la machine ne peut pas les calculer. C’est là que les séries numériques entrent en jeu, elles permettent de générer des fonctions pour le calcul des fonctions non numériques, on peut voir la formule en bas par exemple la fonction cosinus, sinus, cosinus hyperbolique et sinus hyperbolique sous format de série numérique.
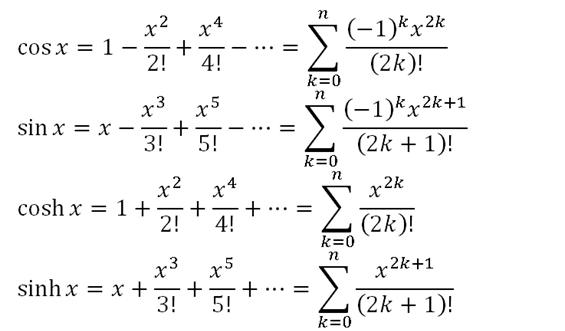
La vidéo suivante montre un enseignant entrain de faire en live sur une période de 6 heurs d’affilée la solution de l’étude de la convergence de 100 séries à la suite et sans s’arrêter. L’étude de la convergence d’une série est très importante, ça permet de dire si la série est potentiellement une fonction génératrice si elle converge. C’est bonne méthode d’apprendre et de réviser pour les examens.


