Algorithmique et Structure de Données

L’algorithme de la recherche dichotomique

La recherche dichotomique, ou encore bien connu en anglais sous le nom de “Binary search”, est un algorithme de recherche bien connu en académie et surtout bien implanté dans le domaine pratique. Ça s’apparente aux arbres binaires dont j’ai récemment écrit un article les concernant. Ils sont apparentés dans le sens où les arbres binaires peuvent implémenter efficacement l’algorithme de la recherche dichotomique.

La vidéo en bas de la chaîne YouTube Computerphile expose très bien le concept de l’algorithme, et même que l’idée derrière cet algorithme est assez simple et intuitive. Supposons un ensemble où vous avez des valeurs ou des entrées ordonnées, comme par exemple un dictionnaire, où les entrées sont ordonnées par ordre alphabétique. La méthode la moins efficace pour chercher un mot est de parcourir les entrées une à une du début à la fin du dictionnaire. Mais en réalité, il est plus optimal de commencer la recherche au milieu. En sachant que les entrées sont ordonnées, vous pouvez deviner si la valeur recherchée se trouve dans la moitié inférieure ou dans la moitié supérieure. Vous venez ainsi d’éliminer le temps de recherche sur la moitié de l’ensemble. Et le processus ensuite va se répéter récursivement pour la moitié restante jusqu’à arriver précisément à trouver la position de votre valeur. C’est ainsi le principe de fonctionnement de la recherche dichotomique.

Algorithme de recherche dichotomique

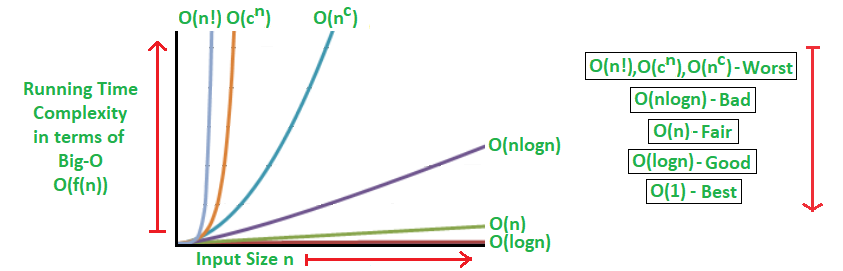
Théoriquement, cette méthode peut à première vue sembler peu efficace, mais en réalité elle est très très puissante. Si par exemple vous avez un dictionnaire d’un million d’entrées, dans le pire des cas, vous aurez à faire 20 opérations pour trouver votre valeur. Alors que dans une recherche avec la méthode basique de parcourir toutes les entrées, dans le pire des cas, vous aurez à faire un million d’opérations. Entre 20 opérations et un million d’opérations il n’y a pas photo, clairement l’algorithme est très efficace. Et ça l’est encore plus avec des ensembles plus grands, puisque la complexité de cet algorithme est logarithmique. C’est vrai que ça semble vertigineux, si vous ne me croyez pas, vous pouvez tester ça vous-même, en utilisant une calculatrice et en divisant la valeur un million par 2, 20 fois.

La complexité d’un algorithme

Pour concevoir des logiciels bien optimisés, il est souvent nécessaire de pouvoir distinguer les algorithmes optimaux des algorithmes trop gourmands en ressources. D’où l’entrée en jeu de l’étude de la complexité d’un algorithme, qui devient primordiale pour reconnaître son optimalité dans le monde réel. En d’autres mots, ça permet de prédire le comportement d’un algorithme avec un nombre très élevé de données.

Pour avoir une compréhension de c’est quoi la complexité d’un algorithme, appelez aussi le grand-O (Big-O en anglais), on va imaginer un exemple simple, supposons qu’un algorithme nécessite une seconde pour calculer 10 données, sa complexité est monotone (O(n)) s’il lui faudrait 10 secondes pour finir 100 données. Par contre si c’est un algorithme optimal il lui faudrait moins de temps. Ou inversement si c’est un algorithme gourmand il lui faudrait plus. La complexité permet plus ou moins de prédire ce temps.

Notion du Big-O (par www.geeksforgeeks.org)

À vrai dire, l’étude de la complexité est une méthode mathématique relativement difficile à appréhender à première vue. La principale raison est que cette méthode ne ressemble à aucun domaine mathématique vu auparavant dans le cursus de l’étudiant. On peut grossièrement la qualifier comme un point d’intersection entre le calcul arithmétique et le calcul des limites dans l’analyse mathématique. D’une part, malgré que le but de la méthode soit le calcul du temps nécessaire pour l’exécution en rapport avec les données exercées sur l’algorithme, elle ne va pas faire un calcul arithmétique exacte de ce temps comme on avait vu sur l’exemple, mais elle va plutôt nous fournir une approximation. Et d’autre part la méthode tend à évaluer le temps pour un nombre très grand de données, et s’appuyer sur des procédés mathématiques qui sont similaires au calcul des limites, comme par exemple négliger les fonctions les moins rapides (comme par exemple : 2X²+ 4X +1 tend vers X²). Mais en même temps, ce n’est pas un calcul de limite. La complexité va réellement nous retourner une fonction parmi les fonctions illustrées sur le graphe en haut. Cette fonction va nous donner une estimation de la rapidité en complexité de l’algorithme en rapport avec le nombre de données. La vidéo en bas de la chaîne YouTube du site web éducatif www.freecodecamp.org illustre cette notion de complexité sous format d’un cours de courte durée pour appréhender plus ou moins cette notion du Big-O.

Cours sur la complexité d’algorithme

Les listes chaînées

Un domaine bien connu en informatique c’est les structures de données, c’est une science dans laquelle les données à l’intérieur de la machine sont organisées d’une manière particulaire pour les rendre plus optimales pour certaines opérations ou certains algorithmes. Les listes chaînées comme structures de données sont très connues, ce sont le concurrent direct des fameux tableaux, un tableau est construit lorsque plusieurs données sont mises en contigus l’une à coté de l’autre dans la mémoire, alors que les listes chaînées c’est tout l’inverse, c’est des données dispersées dans la mémoire avec un moyen de les enchaîner l’une à l’autre. Pratiquement toutes les opérations faisables sur les tableaux sont aussi faisables sur les listes chaînées, le programmeur ou l’étudiant lorsqu’il est mené à choisir entre l’une des deux structures, normalement il doit choisir par rapport aux types d’opérations qui veut effectuer sur les données, si le programme fait beaucoup d’opérations d’ajout et de suppression qui vont modifier l’ensemble des données, là c’est les listes qui sont préférées, dans le cas contraire, lorsque l’ensemble est fixe dans sa taille et il y a beaucoup d’accès et de modification des données, là c’est les tableaux. La vidéo suivante est celle de la chaîne CS Dojo, les principaux concepts des listes sont expliqués et l’implémentation est faute en langage Java.

Introduction au listes chaînées

Introduction aux structures de données

Encore un autre cours sur les structures de données, d’autre part c’est très important, le cours sur la vidéo en bas est très court, la vidéo ne dure que 3 heures avec un survol sur les principales structures de données. Pour rappel, cette matière éducative traite les différentes manières d’organiser et d’arranger les données dans la mémoire pour une utilisation optimale dans la programmation, il existe plusieurs structures, chaque une d’elles a ses avantages et ses inconvénients en dépend de la nature du problème et de l’algorithme utilisé.

Cours sur les structures de données

L’auteur au début de la vidéo fait une bonne introduction sur la notion de la complexité (big O), il continue ensuite en séquence par donner de bonnes explications sur les différentes structures, sans pour autant aborder leurs implémentations et programmation, les structures abordées en question sont ; les tableaux, les vecteurs (tableaux à taille variable, appelés dans la vidéo ArrayList), les piles, les files, les listes chaînées, les listes doublement chaînées, les maps (appelés dans la vidéo dictionary), les arbres avec trois variantes, les arbres binaires de recherches, les tries (arbres pour stocker les mots d’un dictionnaire), les tas (appelés dans la vidéo heap), en terminant avec les graphes.

La vidéo est celle de la chaîne Youtube FreeCodeComp.org, la chaîne appartient au site-web éducatif du même nom, la chaîne dispose d’un nombre important de vidéos didactiques et tutoriel de très bonnes qualités sur différents aspects de l’informatique.

Cours sur les structures de données

La vidéo suivante concerne les structures de données, c’est une très bonne vidéo dans le domaine de l’algorithmique, celle-ci est produite par un ingénieur de Google du nom de William Fiset (voici sa chaine Youtube). La vidéo prend en tout plus de 8 heures, parcourant les concepts et les modèles de structures de données les plus connus d’une façon croissante, du plus simple commençant par les tableaux aux plus complexes terminant par les files à priorité indexées.

Structures de données

Dans sa globalité, la narration est très bonne, comme toutes les vidéos de la chaine Youtube du site FreeCodeCamp.org d’ailleurs. Le narrateur aborde ces concepts qui sont le plus souvent complexes, d’une façon structurée avec un rythme constant et soutenu d’accroissement de difficulté de telle sorte que l’auditeur arrive à suivre sans difficulté. Néanmoins ça reste de l’algorithmique et ça demande toujours des pauses pour des temps de réflexion.

Le langage utilisé pour l’implémentation de ces concepts est le Java, et personnellement j’ai trouvé ça désolant, le langage C ou C++ aurait été plus approprié à mon avis, sachant que ces deux langages permettent d’accentuer l’analyse sur les notions comme les pointeurs et la gestion dynamique de la mémoire qui sont cachés et faite d’une manière automatique par Java.

Il est aussi important de dire que la vidéo représente effectivement un parcours relativement approfondi sur les structures de données, mais pour bien maîtriser ces concepts, elle ne peut en aucun cas replacer la pratique par plusieurs exercices et l’implémentation réel de plusieurs programmes sur machine, et surtout faire face à de vraies erreurs de programmation et avoir à faire potentiellement du débogage sur les programmes, qui sont très bénéfiques pour ce genre de concepts.

500+ exercices en Algorithmique et Structure de Données

Exercices en Algorithmique et Structure de Données

Il est bien connu lors du processus d’apprentissage en informatique, que pour bien assimiler les deux modules fondamentaux; Algorithmique et Structure de Données, et Conception Hardware, qu’il faut bien s’exercer et résoudre différents types de problèmes. le site Techie Delight répertorie pas moins de 500 problèmes dans l’Algorithmique et Structure de Données couvrant différentes facettes du module, comme: les tableaux, les matrices, les chaînes de caractères, les listes chaînées, les files, les piles, les arbres, les arbres binaires, les tas, les graphes, la récursivité, les algorithmes de manipulation de bits, de tri, de hachage, la programmation dynamique…etc. Le site inclut des aspects avancés de la programmation, maîtrisant les 500+ exercices apporte une énorme expérience dans le domaine.